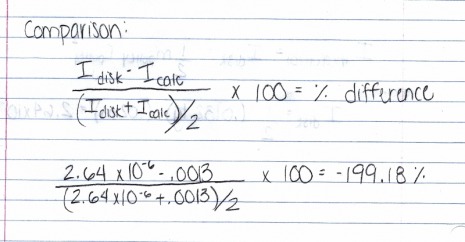Tamara- AP Physics
Rotational Motion Lab
Purpose:
Measure the translational acceleration of a object falling from a pulley and use the measured acceleration to analyze the validity of assumption that the pulley exhibits rotational inertia consistent with a disk (I = ½ MR2).
Equipment:
Pulley
hanging mass
notecard (so the motion detector would register the object)
motion detector with CBL data acquisition system
LoggerPro
Measure the translational acceleration of a object falling from a pulley and use the measured acceleration to analyze the validity of assumption that the pulley exhibits rotational inertia consistent with a disk (I = ½ MR2).
Equipment:
Pulley
hanging mass
notecard (so the motion detector would register the object)
motion detector with CBL data acquisition system
LoggerPro
Procedure
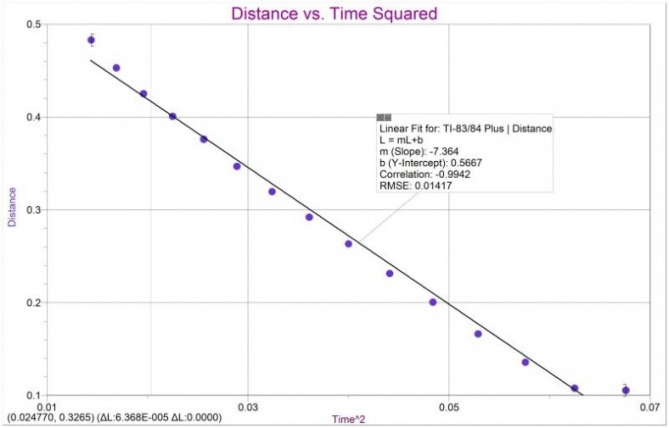
We set up a pulley device on the edge of our station. We attached an object to the end of the string. Next, we set up the motion detector device directly below the pulley system to measure distance and time data. In order for the motion detector to register the object, we had to attach a note card to the object as shown in the picture above. We had to drop the object many times before we got appropriate data. Once we got an acceptable graph on the calculator, we used LoggerPro to produce the target graph and the best-fit line. By doing so, we were able to compute the acceleration of the object.
We set up a pulley device on the edge of our station. We attached an object to the end of the string. Next, we set up the motion detector device directly below the pulley system to measure distance and time data. In order for the motion detector to register the object, we had to attach a note card to the object as shown in the picture above. We had to drop the object many times before we got appropriate data. Once we got an acceptable graph on the calculator, we used LoggerPro to produce the target graph and the best-fit line. By doing so, we were able to compute the acceleration of the object.
Data
Distance
0.482848
0.452861
0.425095
0.400661
0.37595
0.346795
0.319585
0.292097
0.26322
0.231289
0.200469
0.166317
0.135775
0.107731
0.10551
0.482848
0.452861
0.425095
0.400661
0.37595
0.346795
0.319585
0.292097
0.26322
0.231289
0.200469
0.166317
0.135775
0.107731
0.10551
Time ²
0.0144
0.0169
0.0196
0.0225
0.0256
0.0289
0.0324
0.0361
0.04
0.0441
0.0484
0.0529
0.0576
0.0625
0.0676
0.0144
0.0169
0.0196
0.0225
0.0256
0.0289
0.0324
0.0361
0.04
0.0441
0.0484
0.0529
0.0576
0.0625
0.0676
Data Analysis
During the analysis process, we had to find the moment of inertia. We calculated the moment of inertia to be .0013. Then, we had to find what the moment of inertia actually should be. The product was 2.64 x 10^-6. This is not the same as our initial calculation. we, then had to find the difference between the two calculations using the formula below. The difference between the moments of inertial was -199.18%.
Conclusion
Our group encountered an enormous amount of error because our calculations were off. We had an acceleration much greater than gravity. This problem could be due to the "noise" the detector was picking up, or simply human error. The first few times we dropped the object, the detector was not picking up accurate data. Human error is a definite possibly. This could include timing, measurement error, and, even, calculation error. If any of these problems occur, the final product is greatly affected. Although our calculations are off, we did grasp the concept of the lab. In this lab, we did calculate the translational acceleration is the angular acceleration times the radius, but we failed to prove the pulley rotational motion was consistent to the disk using our data.
The data proved an overall obstacle, but we continued to calculate. Doing this allowed the group to see what went wrong. It, also, allowed us to compute the difference to prove our problems. With these problems, the group got a first-hand look at how easy it is for an error to occur. We will have to be more careful, and observe all variables in order to acquire proper data.
This lab, even though our group got faulty data, helped me learn relationships between rotational and translational motions.
Side note:
We, also, learned that listening to the instructions can be a huge help. :)
Our group encountered an enormous amount of error because our calculations were off. We had an acceleration much greater than gravity. This problem could be due to the "noise" the detector was picking up, or simply human error. The first few times we dropped the object, the detector was not picking up accurate data. Human error is a definite possibly. This could include timing, measurement error, and, even, calculation error. If any of these problems occur, the final product is greatly affected. Although our calculations are off, we did grasp the concept of the lab. In this lab, we did calculate the translational acceleration is the angular acceleration times the radius, but we failed to prove the pulley rotational motion was consistent to the disk using our data.
The data proved an overall obstacle, but we continued to calculate. Doing this allowed the group to see what went wrong. It, also, allowed us to compute the difference to prove our problems. With these problems, the group got a first-hand look at how easy it is for an error to occur. We will have to be more careful, and observe all variables in order to acquire proper data.
This lab, even though our group got faulty data, helped me learn relationships between rotational and translational motions.
Side note:
We, also, learned that listening to the instructions can be a huge help. :)